Color transformation

This record is just for future references.

Some time ago, I got profiles of transmissivity of our new set of photometric UBRVI filters (thx to K.Navrátil). The filters are offered as a part of the official SBIG's accessories. Profiles of trasmissivity of the filter set and Landolt's (Astron. J. 104, 340 (1992)) filter set is displayed on the image: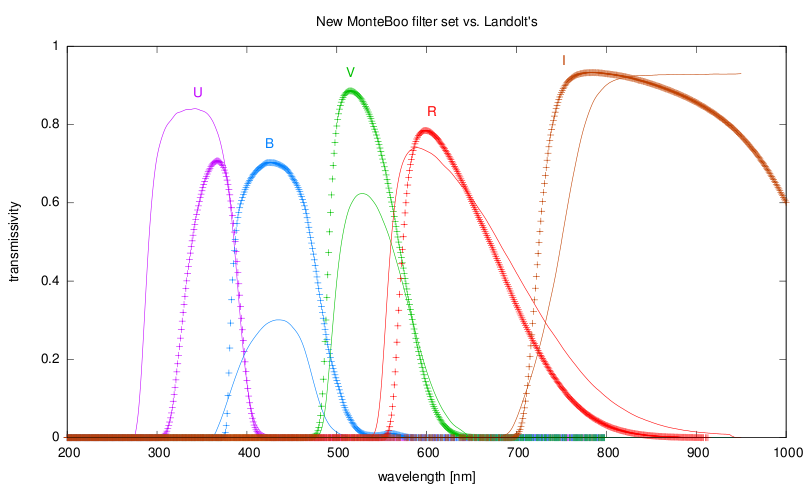(in PDF). All filter profiles together with various useful files are included in archive newfilters.tar.gz.

A knowledge of the profiles enable us to create a transformation between our and Landolt's filters set. The transformation is constructed only on base of the filter's transmissivity. That means that another one made as a product of a real measurement will perhaps different due to any different spectral sensitivities of others parts of our optical equipment (mainly telescope, detector and atmosphere). We are use the transformation between our set {|u>,|b>,|v>,|r>,|i>} and Landolt's {|U>,|B>,|V>,|R>,|I>} as the matrix equation

|u> = U><U|u> + |B><B|u> + |V> <V|u> + |R><R|u> + |I><I|u>
|b> = U><U|b> + |B><B|b> + |V> <V|b> + |R><R|b> + |I><I|b>
|v> = U><U|v> + |B><B|v> + |V> <V|v> + |R><R|v> + |I><I|v>
|r> = U><U|r> + |B><B|r> + |V> <V|r> + |R><R|r> + |I><I|r>
|i> = U><U|i> + |B><B|i> + |V> <V|i> + |R><R|i> + |I><I|i>

where the matrix elements are defined as area determined by the product of the transmissivity of the filters. For example

<U|u> = ʃ U(λ)u(λ) dλ
<B|u> = ʃ B(λ)u(λ) dλ

...

for all wavelengths λ = 0 to ∞. The results of the integration and solution of the matrix equation are in the table:

0.5051 -0.0131 -0.0008 -0.0001 -0.0000
0.1680 2.5373 0.0233 0.0028 0.0008
-0.0010 0.0587 1.4170 -0.1299 -0.0381
0.0003 -0.0104 -0.0828 0.9252 0.0747
-0.0000 0.0009 0.0073 -0.0460 1.0063

The filter based transformation between our instrumental magnitudes m_i for i = U,B,V,R,I and Landolt's M_i is described by the term

m_u - M_U =
-2.5( log10 <U|u> + log e (<B|u> + <V|u>+<R|u>+<I|u>)/<U|u>)
+ <B|u>/<B|b> (M_B - M_U)
+ <V|u>/<B|b> (M_V - M_U)
+ <R|u>/<B|b> (M_R - M_U)
+ <I|u>/<B|b> (M_I - M_U)
...

(analogically for other filters). The numerical results are:

m_u - m_U = 0.8110 - 0.0260 (m_B - m_U) - 0.0016 (m_V - m_U) - 0.0002 (m_R - m_U)

m_b - m_B = -1.203 + 0.0662 (m_U - m_B) + 0.0092 (m_V - m_B) + 0.0011 (m_R - m_B) + 0.0003 (m_I - m_B)

m_v - m_V = -0.1838 - 0.0007 (m_U - m_V) + 0.0415 (m_B - m_V) - 0.0917 (m_R - m_V) - 0.0269 (m_I - m_V)

m_r - m_R = 0.1338 + 0.0003 (m_U - m_R) -0.0113 (m_B - m_R) - 0.0895 (m_V - m_R) + 0.0807 (m_I - m_R)

m_i - m_I = 0.0870 + 0.0009 (m_B - m_I) + 0.0073 (m_V - m_I) - 0.0457 (m_R - m_I)

Detailed description of the used method and an application to our old
filters can be found in Janis's bachelor work (in Czech).

(The old school typhographics rules! A "modern" graphics technologies doesn't supports a little bit complicated typesetting as (La)TeX did twenty years ago.)