On principal pitfall of a star's magnitude calibration

A calibration of magnitudes of an instrumental system to a standard system by an aperture photometry method should be revealing of some unexpected behaviour. Very bright stars are calibrated successfully (also the widely-known method of measuring of an extinction – Bouguer line – gives good results), but fainter (and faintest) stars are exhibiting of some horrible scattering, eg. they're not usable for the calibration. I think, it's result of any inaccurate determination of a sky background. Although our methods for the sky determination are more advanced. The inaccuracy comes from an unstable character of the problem of the aperture photometry.

To show, how some tiny inaccuracy in the background determination fluences to a resultant flux, we will suppose that stars are represented by Gaussian profile

G = G0*exp(-r**2).

An integration in polar coordinates (Jacobian!) of the profile gives us a total flux

F = F0*[1 - exp(-r**2)]

The flux F is equivalent to quantity coming from the aperture photometry, eg. the method which we're uses to estimate of the instrumental magnitude. The real situation is different. We need to subtract the background before summing (integration) of the detected signal on our CCD matrix. The model of detected signal may easy described by

I = G0*exp(-r**2) + B

where B is a constant added to every pixel. It's due to an illumination of the chip by a night sky or any another source. To get aperture photometry, we need subtract of B. That means, that we need to estimate of B by a statistical method with some uncertainty b (b << B).

Let's look to details of determination of total flux with a small error of B estimation. We have a function

I = G0*exp(-r**2) + (B + b)

and subtraction of B leads to

I' = G0*exp(-r**2) + b

so the total measurable flux F' (directly measurable by the aperture photometry) will be

F' = F0*[1 - exp(-r**2)] + π*b*r**2.

This is key moment. Our pitfall is presence of a second term. The first term is total flux of the source and its value is finite and physically limited at any radii. Note that choice of the analytic description of the term is not important. We only requires of integrable function, eg. its integral isn't infinite. Integrable functions has also an appropriate physical meaning. The size of second term depends on uncertainty of estimate of B and on its aperture's area. Because first term is limited, there is a radius where second term dominates over first. The radius depends on the inaccuracy of estimation of B and on object's brightness.

The important characteristics of the measured total flux is its instability. An instability in usual sense means strong dependence of results on input parameters. That is our case. Any tiny (small) perturbation of B lead to strong deviation of output from profile. And, what is more worse, any non-zero value of b (eg. all possible measurable cases) has no limit and the results diverge in in any possible cases (limit of F' is the infinity for the b non-zero)! We won't win!

The findings may interpret results of real measurements. Fluxes of bright stars are (in small apertures) not affected by second term. Faint stars may be too faint and the second term may by more important than the first one at small radii.

Theoretical disturbed profiles

To test the hypothesis, I prepared some graphs. The first one shows of the flux F' of an artificial Gaussian profile disturbed by values of background in range -0.1 to 0.1 (±10%). Both axes takes relative units. The graph is a nice demonstration of drastic fluency of any background estimation error on its resultant profile. Two most important characteristics of error of background estimation are:

• any non-zero value induce significant change of shape of profile
• profile has no limit in infinity

Leo I annotated

Leo I with removed stars

My second graph represents more real situation. There are disturbed fitted profiles of stars on the image of Leo I. The most important change to previous one are:

• magnitude scale
• the profile is non-Gaussian

Set of disturbed profiles of stars on Leo I

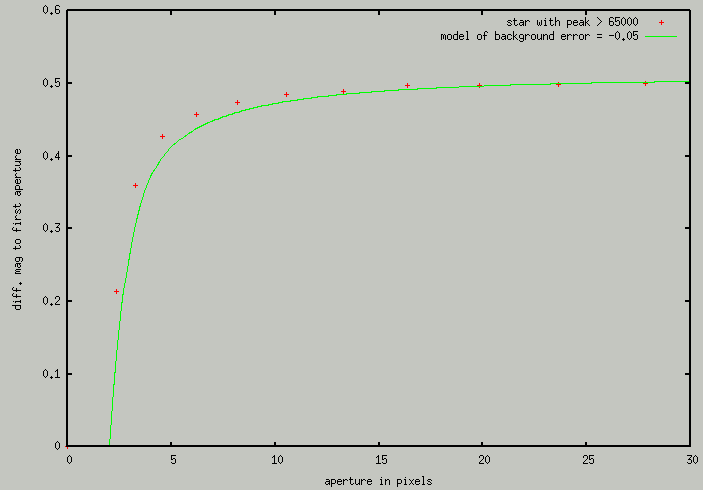
The vertical scale shows differences in magnitudes with respect to first aperture. The profile is modelled by a complex function as composition of wighted sum of Gaussian, Moffat and exponential function (see Stetson (1990)). The reliability of the fit can be demonstrated by another image on which the stars has been removed on base of the profile.

Profile of a bright star #1

Final pair of images shows an application of the disturbed mean profiles for two stars. The bright star has no warped profile. Any uncertainty in the sky estimation is insignificant to the total measurable flux of the star. The star is designed by #1 in the above image. The profile shows systematic differences in small radii. It is perhaps due to saturation of the star (the maximum of peak is greater than photon capacity of our CCD detector).

Profile of a faint star #2

The graph for faint star #2 clearly exhibits the effect of the error in estimation of the sky. The profile can be satisfactory modeled if we subtract 0.05 ADU (b = -0.05) from the sky background (determined by Munipack's). We can see, that the precision of the determination of the sky is really important for relative faint stars with its peak only about six thousands and the sky value about six hundredth (ten percent only!). A last point at radius 28 is affected by a hot pixel. The really interesting effects is the deviation of measured values and the modeled profile. The deviation shows some scattering in order of hundredth of magnitude (which corresponds to the precision given by photon statistics). But more important is relative difference between bright and faint star. We can see that the difference depends on aperture which has been used for estimation of magnitude of stars. That means that any magnitude calibration to standard system will depend on magnitude of the star. That is really poor property of the aperture photometry.

Note, that I selected the stars very carefully, because profiles of faint stars are strongly affected by various kinds of defects.

Another point of view offers photon statistics. The middle bright star on the CCD chip gives typically 10^5 photons, so the statistical uncertainty due to only Poisson noise gives about 0.003 magnitude which is about ten factor better than is usually measured.

The key thing of the post (strong fluency of background on aperture magnitudes) is included in paper of Howell (1989). There is only extension some theoretical ideas and another practical test.